|
|
|

A Fractal derived from the Koch Snowflake. The base curve and motif for the fractal are illustrated below.
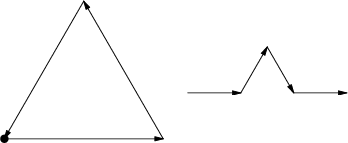
The Area after the ![]() th iteration is
th iteration is
See also Exterior Snowflake, Flowsnake Fractal, Koch Snowflake, Pentaflake, Sierpinski Curve
References
Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 66-67, 1989.
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton
University Press, pp. 36-37, 1991.
![]() Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.
Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.