|
|
|
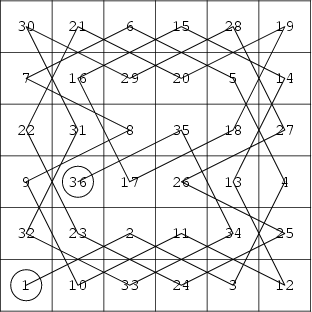
A knight's tour of a Chessboard (or any other grid) is a sequence of moves by a knight Chess piece (which may
only make moves which simultaneously shift one square along one axis and two along the other) such that each square of the
board is visited exactly once (i.e., a Hamiltonian Circuit). If the final position is a knight's move away from the
first position, the tour is called re-entrant. The first figure above shows a knight's tour on a ![]() Chessboard.
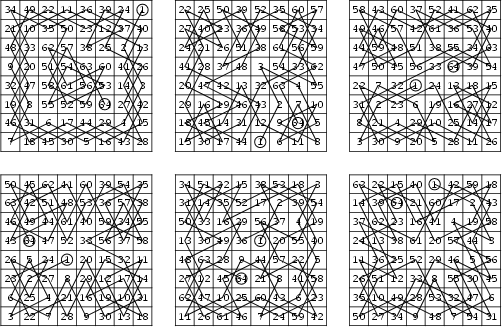
The second set of figures shows six knight's tours on an
Chessboard.
The second set of figures shows six knight's tours on an ![]() Chessboard, all but the first of which are
re-entrant. The final tour has the additional property that it is a Semimagic Square with row and column sums of 260 and
main diagonal sums of 348 and 168.
Chessboard, all but the first of which are
re-entrant. The final tour has the additional property that it is a Semimagic Square with row and column sums of 260 and
main diagonal sums of 348 and 168.
Löbbing and Wegener (1996) computed the number of cycles covering the directed knight's graph for an ![]() Chessboard. They obtained
Chessboard. They obtained ![]() , where
, where
![]() , i.e., 8,121,130,233,753,702,400. They also
computed the number of undirected tours, obtaining an incorrect answer 33,439,123,484,294 (which is not divisible by 4 as
it must be), and so are currently redoing the calculation.
, i.e., 8,121,130,233,753,702,400. They also
computed the number of undirected tours, obtaining an incorrect answer 33,439,123,484,294 (which is not divisible by 4 as
it must be), and so are currently redoing the calculation.
The following results are given by Kraitchik (1942). The number of possible tours on a ![]() board for
board for ![]() , 4,
... are 8, 0, 82, 744, 6378, 31088, 189688, 1213112, ... (Kraitchik 1942, p. 263). There are 14 tours on the
, 4,
... are 8, 0, 82, 744, 6378, 31088, 189688, 1213112, ... (Kraitchik 1942, p. 263). There are 14 tours on the ![]() rectangle, two of which are symmetrical. There are 376 tours on the
rectangle, two of which are symmetrical. There are 376 tours on the ![]() rectangle, none of which is closed. There
are 16 symmetric tours on the
rectangle, none of which is closed. There
are 16 symmetric tours on the ![]() rectangle and 8 closed tours on the
rectangle and 8 closed tours on the ![]() rectangle. There are 58 symmetric
tours on the
rectangle. There are 58 symmetric
tours on the ![]() rectangle and 28 closed tours on the
rectangle and 28 closed tours on the ![]() rectangle. There are five doubly symmetric tours
on the
rectangle. There are five doubly symmetric tours
on the ![]() square. There are 1728 tours on the
square. There are 1728 tours on the ![]() square, 8 of which are symmetric. The longest
``uncrossed'' knight's tours on an
square, 8 of which are symmetric. The longest
``uncrossed'' knight's tours on an ![]() board for
board for ![]() , 4, ... are 2, 5, 10, 17, 24, 35, ... (Sloane's A003192).
, 4, ... are 2, 5, 10, 17, 24, 35, ... (Sloane's A003192).
See also Chess, Kings Problem, Knights Problem, Magic Tour, Queens Problem, Tour
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York:
Dover, pp. 175-186, 1987.
Chartrand, G. ``The Knight's Tour.'' §6.2 in Introductory Graph Theory. New York: Dover, pp. 133-135, 1985.
Gardner, M. ``Knights of the Square Table.'' Ch. 14 in
Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American.
New York: Vintage, pp. 188-202, 1978.
Guy, R. K. ``The
Kraitchik, M. ``The Problem of the Knights.'' Ch. 11 in Mathematical Recreations. New York: W. W. Norton,
pp. 257-266, 1942.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 87-89, 1979.
Ruskey, F. ``Information on the
Sloane, N. J. A. Sequences
A003192/M1369
and A006075/M3224
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
van der Linde, A. Geschichte und Literatur des Schachspiels, Vol. 2. Berlin, pp. 101-111, 1874.
Volpicelli, P. ``Soluzione completa e generale, mediante la geometria di situazione, del problema relativo alle corse del cavallo sopra
qualunque scacchiere.'' Atti della Reale Accad. dei Lincei 25, 87-162, 1872.
Wegener, I. and Löbbing, M. ``The Number of Knight's Tours Equals 33,439,123,484,294--Counting with Binary
Decision Diagrams.'' Electronic J. Combinatorics 3, R5 1-4, 1996.
http://www.combinatorics.org/Volume_3/volume3.html#R5.
![]() Queens Problem.'' §C18 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 133-135, 1994.
Queens Problem.'' §C18 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 133-135, 1994.
![]() Knight's Tour Problem.''
http://sue.csc.uvic.ca/~cos/inf/misc/Knight.html.
Knight's Tour Problem.''
http://sue.csc.uvic.ca/~cos/inf/misc/Knight.html.
|
|
|
© 1996-9 Eric W. Weisstein