If a Real curve has no singularities except nodes and Cusps, Bitangents, and
Inflection Points, then
where 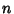 is the order,
is the order, 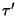 is the number of conjugate tangents,
is the number of conjugate tangents, 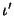 is the number of Real
inflections,
is the number of Real
inflections, 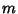 is the class,
is the class, 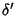 is the number of Real conjugate points, and
is the number of Real conjugate points, and 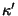 is the
number of Real Cusps. This is also called Klein's Theorem.
is the
number of Real Cusps. This is also called Klein's Theorem.
See also Plücker's Equation
References
Coolidge, J. L. A Treatise on Algebraic Plane Curves. New York: Dover, p. 114, 1959.
© 1996-9 Eric W. Weisstein
1999-05-26