|
|
|
An Auxiliary Latitude which is directly proportional to the spacing of parallels of
Latitude from the equator on an ellipsoidal Mercator Projection. It is defined by
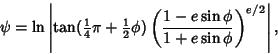 |
(1) |
| (2) |
![\begin{displaymath}
\phi=2\tan^{-1}\left[{\mathop{\rm exp}\nolimits (\psi)\left(...
...r 1-e\sin\phi}\right)^{e/2}}\right]-{\textstyle{1\over 2}}\pi,
\end{displaymath}](i_1319.gif) |
(3) |
| (4) |
See also Latitude
References
Adams, O. S. ``Latitude Developments Connected with Geodesy and Cartography with Tables, Including a Table for
Lambert Equal-Area Meridional Projections.'' Spec. Pub. No. 67. U. S. Coast and Geodetic Survey, 1921.
Snyder, J. P. Map Projections--A Working Manual. U. S. Geological Survey Professional Paper 1395. Washington,
DC: U. S. Government Printing Office, p. 15, 1987.