|
|
|
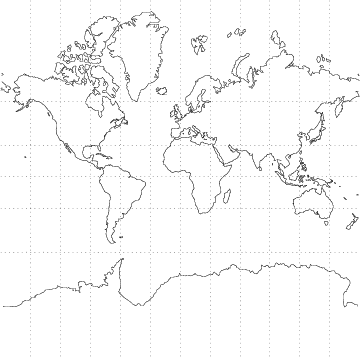
The following equations place the x-Axis of the projection on the equator and the
y-Axis at Longitude ![]() , where
, where ![]() is the Longitude and
is the Longitude and ![]() is the
Latitude.
is the
Latitude.
| (1) | |||
| (2) | |||
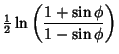 |
(3) | ||
| (4) | |||
| (5) | |||
| (6) |
| (7) | |||
| (8) |
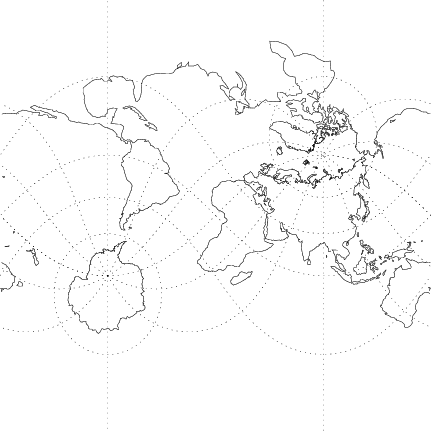
An oblique form of the Mercator projection is illustrated above. It has equations
![$\displaystyle {\tan^{-1}[\tan\phi\cos\phi_p+\sin\phi_p\sin(\lambda-\lambda_0)]\over\cos(\lambda-\lambda_0)}$](m_968.gif) |
(9) | ||
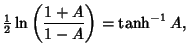 |
(10) |
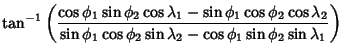 |
|||
| (11) | |||
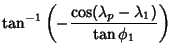 |
(12) | ||
| (13) |
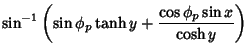 |
(14) | ||
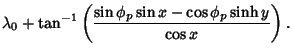 |
(15) |
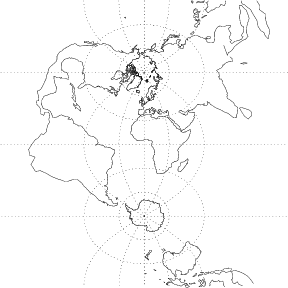
There is also a transverse form of the Mercator projection, illustrated above. It is given by the equations
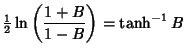 |
(16) | ||
![$\displaystyle \tan^{-1}\left[{\tan\phi\over \cos(\lambda-\lambda_0)}\right]-\phi_0$](m_980.gif) |
(17) | ||
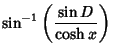 |
(18) | ||
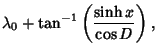 |
(19) |
| (20) | |||
| (21) |
Finally, the ``universal transverse Mercator projection'' is a Map Projection which maps the Sphere into 60 zones of 6° each, with each zone mapped by a transverse Mercator projection with central Meridian in the center of the zone. The zones extend from 80° S to 84° N (Dana).
See also Gudermannian Function, Spherical Spiral
References
Dana, P. H. ``Map Projections.''
http://www.utexas.edu/depts/grg/gcraft/notes/mapproj/mapproj.html.
Snyder, J. P. Map Projections--A Working Manual. U. S. Geological Survey Professional Paper 1395.
Washington, DC: U. S. Government Printing Office, pp. 38-75, 1987.
|
|
|
© 1996-9 Eric W. Weisstein