|
|
|
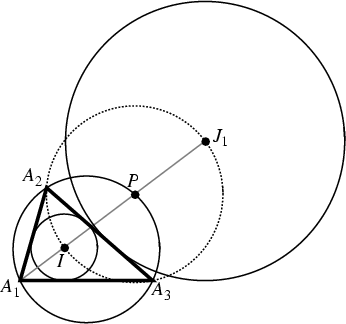
Given a triangle
![]() , the points
, the points ![]() ,
, ![]() , and
, and ![]() lie on a line, where
lie on a line, where ![]() is the Incenter and
is the Incenter and ![]() is the Excenter corresponding to
is the Excenter corresponding to ![]() . Furthermore, the Circle with
. Furthermore, the Circle with ![]() as the Diameter has
as the Diameter has ![]() as its center, where
as its center, where ![]() is the intersection of
is the intersection of ![]() with the Circumcircle of
with the Circumcircle of
![]() , and passes through
, and passes through
![]() and
and ![]() . This Circle has Radius
. This Circle has Radius
See also Circumcircle, Excenter, Excenter-Excenter Circle, Incenter, Orthocentric System
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, p. 185, 1929.