|
|
|
A Tessellation in ![]() -D, for
-D, for ![]() . The only regular honeycomb in 3-D is
. The only regular honeycomb in 3-D is ![]() , which consists of eight
cubes meeting at each Vertex. The only quasiregular honeycomb (with regular cells and
semiregular Vertex Figures) has each Vertex surrounded by eight
Tetrahedra and six Octahedra and is denoted
, which consists of eight
cubes meeting at each Vertex. The only quasiregular honeycomb (with regular cells and
semiregular Vertex Figures) has each Vertex surrounded by eight
Tetrahedra and six Octahedra and is denoted
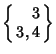 .
.
There are many semiregular honeycombs, such as
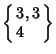 , in which each
Vertex consists of two Octahedra
, in which each
Vertex consists of two Octahedra ![]() and four
Cuboctahedra
and four
Cuboctahedra
![]() .
.
See also Sponge, Tessellation
References
Bulatov, V. ``Infinite Regular Polyhedra.'' http://www.physics.orst.edu/~bulatov/polyhedra/infinite/.