|
|
|
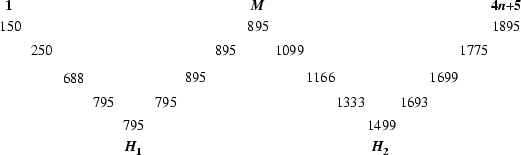
The upper and lower hinges are descriptive statistics of a set of ![]() data values, where
data values, where ![]() is of the form
is of the form ![]() with
with
![]() , 1, 2, .... The hinges are obtained by ordering the data in increasing order
, 1, 2, .... The hinges are obtained by ordering the data in increasing order ![]() , ...,
, ..., ![]() , and writing them out
in the shape of a ``w'' as illustrated above. The values at the bottom legs are called the hinges
, and writing them out
in the shape of a ``w'' as illustrated above. The values at the bottom legs are called the hinges ![]() and
and ![]() (and the
central peak is the Median). In this ordering,
(and the
central peak is the Median). In this ordering,
See also H-Spread, Haberdasher's Problem, Median (Statistics), Order Statistic, Quartile, Trimean
References
Tukey, J. W. Explanatory Data Analysis. Reading, MA: Addison-Wesley, pp. 32-34, 1977.