|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
The sum of Reciprocals of Primes diverges, but
![$\displaystyle \lim_{n\to\infty}\left[{\sum_{k=1}^{\pi(n)} {1\over p_k}-\ln(\ln n)}\right]$](h_111.gif) |
![$\displaystyle \gamma+\sum_{k=1}^\infty \left[{\ln\left({1-{1\over p_k}}\right)+{1\over p_k}}\right]$](h_112.gif) |
||
| (1) |
![\begin{displaymath}
\lim_{n\to\infty}\left[{{1\over n}\sum_{k=1}^n \omega(k)-\ln(\ln n)}\right]=C_1.
\end{displaymath}](h_117.gif) |
(2) |
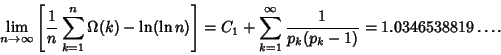 |
(3) |
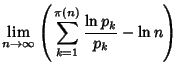 |
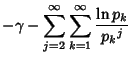 |
||
| (4) |
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/hdmrd/hdmrd.html
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed.
Oxford, England: Clarendon Press, 1985.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 24, 1983.
Rosser, J. B. and Schoenfeld, L. ``Approximate Formulas for Some Functions of Prime Numbers.'' Ill. J. Math. 6, 64-94, 1962.