|
|
|
Let A be an ![]() Real Square Matrix and let
Real Square Matrix and let ![]() and
and ![]() be real numbers with
be real numbers with
![]() . Then Grothendieck showed that there exists a constant
. Then Grothendieck showed that there exists a constant ![]() independent of both A and
independent of both A and ![]() satisfying
satisfying
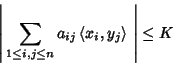 |
(1) |
| (2) |
| (3) |
References
Krivine, J. L. ``Sur la constante de Grothendieck.'' C. R. A. S. 284, 8, 1977.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 42, 1983.