Gray Code

An encoding of numbers so that adjacent numbers have a single Digit differing by 1. A Binary Gray code with $n$ Digits corresponds to a Hamiltonian Path on an $n$-D Hypercube (including direction reversals). The term Gray code is often used to refer to a ``reflected'' code, or more specifically still, the binary reflected Gray code.

To convert a Binary number $d_1\,d_2\cdots\,d_{n-1}\,d_n$ to its corresponding binary reflected Gray code, start at the right with the digit $d_n$ (the $n$th, or last, Digit). If the $d_{n-1}$ is 1, replace $d_n$ by $1-d_n$; otherwise, leave it unchanged. Then proceed to $d_{n-1}$. Continue up to the first Digit $d_1$, which is kept the same since $d_0$ is assumed to be a 0. The resulting number $g_1\,g_2\cdots\,g_{n-1}\,g_n$ is the reflected binary Gray code.

To convert a binary reflected Gray code $g_1\,g_2\cdots\,g_{n-1}\,g_n$ to a Binary number, start again with the $n$th digit, and compute

$$\Sigma_n\equiv \sum_{i=1}^{n-1} g_i {\rm\ (mod\ } 2).$$

If $\Sigma_n$ is 1, replace $g_n$ by $1-g_n$; otherwise, leave it the unchanged. Next compute

$$\Sigma_{n-1}\equiv \sum_{i=1}^{n-2} g_i {\rm\ (mod\ } 2),$$

and so on. The resulting number $d_1\,d_2\cdots\,d_{n-1}\,d_n$ is the Binary number corresponding to the initial binary reflected Gray code.

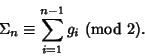
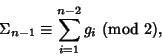
The code is called reflected because it can be generated in the following manner. Take the Gray code 0, 1. Write it forwards, then backwards: 0, 1, 1, 0. Then append 0s to the first half and 1s to the second half: 00, 01, 11, 10. Continuing, write 00, 01, 11, 10, 10, 11, 01, 00 to obtain: 000, 001, 011, 010, 110, 111, 101, 100, ... (Sloane's A014550). Each iteration therefore doubles the number of codes. The Gray codes corresponding to the first few nonnegative integers are given in the following table.

0	0	20	11110	40	111100
1	1	21	11111	41	111101
2	11	22	11101	42	111111
3	10	23	11100	43	111110
4	110	24	10100	44	111010
5	111	25	10101	45	111011
6	101	26	10111	46	111001
7	100	27	10110	47	111000
8	1100	28	10010	48	101000
9	1101	29	10011	49	101001
10	1111	30	10001	50	101011
11	1110	31	10000	51	101010
12	1010	32	110000	52	101110
13	1011	33	110001	53	101111
14	1001	34	110011	54	101101
15	1000	35	110010	55	101100
16	11000	36	110110	56	100100
17	11001	37	110111	57	100101
18	11011	38	110101	58	100111
19	11010	39	110100	59	100110

The binary reflected Gray code is closely related to the solution of the Towers of Hanoi as well as the Baguenaudier.

See also Baguenaudier, Binary, Hilbert Curve, Ryser Formula, Thue-Morse Sequence, Towers of Hanoi

References

Gardner, M. ``The Binary Gray Code.'' Ch. 2 in Knotted Doughnuts and Other Mathematical Entertainments. New York: W. H. Freeman, 1986.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Gray Codes.'' §20.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 886-888, 1992.

Sloane, N. J. A. Sequence A014550 in ``The On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html.

Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 111-112 and 246, 1991.