|
|
|
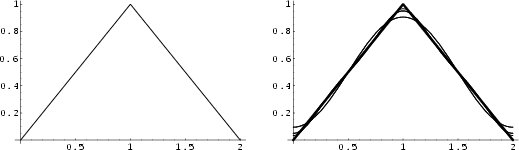
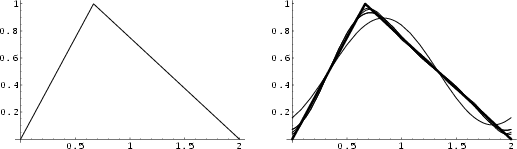
Let a string of length ![]() have a
have a ![]() -displacement of unity when it is pinned an
-displacement of unity when it is pinned an ![]() -distance which is (
-distance which is (![]() )th of the
way along the string. The displacement as a function of
)th of the
way along the string. The displacement as a function of ![]() is then
is then
![$\displaystyle {1\over L}\left[{\int_0^{2L/m} {nx\over 2L}\,dx+\int_{2L/m}^{2L} {n\over 1-n}\left({{x\over 2L}-1}\right)\,dx}\right]$](f_1727.gif) |
|||
![$\displaystyle {m\left[{1-m-\cos(2\pi n)+m\cos\left({2n\pi\over m}\right)}\right]\over 2(m-1)n^2\pi^2}$](f_1728.gif) |
|||
![$\displaystyle {m^2\left[{\cos\left({2n\pi\over m}\right)-1}\right]\over 2(m-1)n^2\pi^2}$](f_1729.gif) |
|||
![$\displaystyle {m\left[{m\sin\left({2\pi n\over m}\right)-\sin(2\pi n)}\right]\over 2(m-1)n^2\pi^2}$](f_1730.gif) |
|||
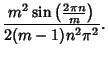 |
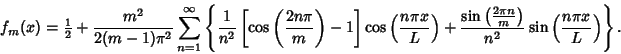
If ![]() , then
, then ![]() and
and ![]() simplify to
simplify to
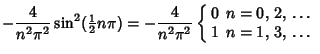 |
|||
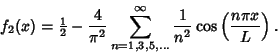
See also Fourier Series