|
|
|

A plane curve proposed by Descartes ![]() to challenge Fermat's
to challenge Fermat's ![]() extremum-finding techniques.
In parametric form,
extremum-finding techniques.
In parametric form,
| (1) | |||
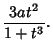 |
(2) |

The Curvature and Tangential Angle of the folium of Descartes, illustrated above, are
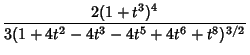 |
(3) | ||
![$\displaystyle {1\over 2}\left[{\pi+\tan^{-1}\left({1-2t^3\over t^4-2t}\right)-\tan^{-1}\left({2t^3-1\over t^4-2t}\right)}\right].$](f_1543.gif) |
|||
| (4) |
Converting the parametric equations to
Polar Coordinates gives
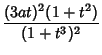 |
(5) | ||
| (6) |
| (7) |
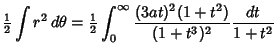 |
|||
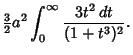 |
(8) |
| (9) |
| (10) |
| (11) |
References
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 59-62, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 106-109, 1972.
MacTutor History of Mathematics Archive. ``Folium of Descartes.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Foliumd.html.
Stroeker, R. J. ``Brocard Points, Circulant Matrices, and Descartes' Folium.'' Math. Mag. 61, 172-187, 1988.
Yates, R. C. ``Folium of Descartes.'' In A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 98-99, 1952.
|
|
|
© 1996-9 Eric W. Weisstein