|
|
|
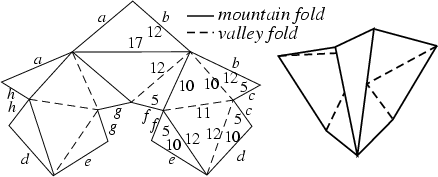
The Rigidity Theorem states that if the faces of a convex Polyhedron are made of metal plates and the Edges are replaced by hinges, the Polyhedron would be Rigid. The theorem was stated by Cauchy (1813), although a mistake in this paper went unnoticed for more than 50 years. Concave polyhedra need not be Rigid, and such nonrigid polyhedra are called flexible polyhedra. Connelly (1978) found the first example of a reflexible polyhedron, consisting of 18 triangular faces. A flexible polyhedron with only 14 triangular faces and 9 vertices (shown above), believed to be the simplest possible composed of only triangles, was subsequently found by Steffen (Mackenzie 1998). There also exists a six-vertex eight-face flexible polyhedron (Wunderlich and Schwabe 1986, Cromwell 1997).
Connelly et al. (1997) proved that a flexible polyhedron must keep its Volume constant (Mackenzie 1998).
See also Polyhedron, Quadricorn, Rigid, Rigidity Theorem
References
Cauchy, A. L. ``Sur les polygones et les polyèdres.'' XVIe Cahier IX, 87-89, 1813.
Connelly, R. ``A Flexible Sphere.'' Math. Intel. 1, 130-131, 1978.
Connelly, R.; Sabitov, I.; and Walz, A. ``The Bellows Conjecture.'' Contrib. Algebra Geom. 38, 1-10, 1997.
Cromwell, P. R. Polyhedra. New York: Cambridge University Press, 1997.
Mackenzie, D. ``Polyhedra Can Bend But Not Breathe.'' Science 279, 1637, 1998.
Wunderlich, W. and Schwabe, C. ``Eine Familie von geschlossen gleichflachigen Polyhedern, die fast beweglich sind.''
Elem. Math. 41, 88-98, 1986.