Fermat's Spiral

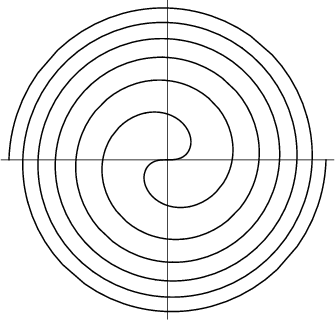
$\begin{figure}\begin{center}\BoxedEPSF{fermats_spiral.epsf}\end{center}\end{figure}$

An Archimedean Spiral with having polar equation

$\begin{displaymath} r = a\theta^{1/2}, \end{displaymath}$

discussed by Fermat

in 1636 (MacTutor Archive). It is also known as the Parabolic Spiral. For any given Positive value of $\theta$ , there are two corresponding values of

of opposite signs. The resulting spiral is therefore symmetrical about the origin. The Curvature is

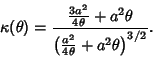
$\begin{displaymath} \kappa(\theta)={{3a^2\over 4\theta}+a^2\theta\over\left({{a^2\over 4\theta}+a^2\theta}\right)^{3/2}}. \end{displaymath}$

References

Dixon, R. Mathographics. New York: Dover, p. 121, 1991.

Lockwood, E. H. A Book of Curves. Cambridge, England: Cambridge University Press, p. 175, 1967.