|
|
|
The Fermat quotient for a number ![]() and a Prime base
and a Prime base ![]() is defined as
is defined as
| (1) |
| (2) | |||
| (3) | |||
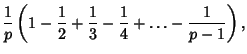 |
(4) |
See also Wieferich Prime
References
Crandall, R. Projects in Scientific Computation. New York: Springer-Verlag, 1986.
Lehmer, D. H. ``On Fermat's Quotient, Base Two.'' Math. Comput. 36, 289-290, 1981.