Given a number 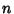 , look for Integers
, look for Integers 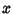 and
and 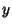 such that
such that 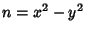 . Then
. Then
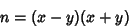 |
(1) |
and 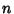 is factored. Any Odd Number can be represented in this form since then
is factored. Any Odd Number can be represented in this form since then 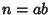 ,
, 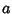 and
and 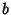 are Odd, and
are Odd, and
Adding and subtracting,
so solving for 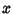 and
and 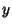 gives
gives
Therefore,
![\begin{displaymath}
x^2-y^2={\textstyle{1\over 4}}[(a+b)^2-(a-b)^2] = ab.
\end{displaymath}](f_491.gif) |
(8) |
As the first trial for 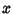 , try
, try
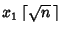 , where
, where
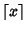 is the Ceiling Function. Then check if
is the Ceiling Function. Then check if
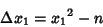 |
(9) |
is a Square Number. There are only 22 combinations of the last two digits which a Square Number can
assume, so most combinations can be eliminated. If 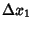 is not a Square Number, then try
is not a Square Number, then try
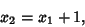 |
(10) |
so
Continue with
so subsequent differences are obtained simply by adding two.
Maurice Kraitchik sped up the Algorithm by looking for 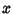 and
and 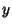 satisfying
satisfying
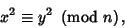 |
(13) |
i.e., 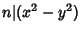 . This congruence has uninteresting solutions
. This congruence has uninteresting solutions
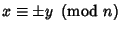 and interesting solutions
and interesting solutions
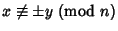 . It turns out that if
. It turns out that if 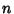 is Odd and Divisible by at least two different
Primes, then at least half of the solutions to
is Odd and Divisible by at least two different
Primes, then at least half of the solutions to
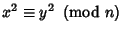 with
with 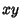 Coprime to
Coprime to 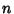 are interesting. For
such solutions,
are interesting. For
such solutions, 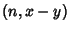 is neither
is neither 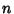 nor 1 and is therefore a nontrivial factor of
nor 1 and is therefore a nontrivial factor of 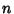 (Pomerance 1996). This
Algorithm can be used to prove primality, but is not practical. In 1931, Lehmer and Powers discovered how to search
for such pairs using Continued Fractions. This method was improved by Morrison and Brillhart
(1975) into the Continued Fraction Factorization Algorithm, which was the fastest Algorithm in use before the
Quadratic Sieve Factorization Method was developed.
(Pomerance 1996). This
Algorithm can be used to prove primality, but is not practical. In 1931, Lehmer and Powers discovered how to search
for such pairs using Continued Fractions. This method was improved by Morrison and Brillhart
(1975) into the Continued Fraction Factorization Algorithm, which was the fastest Algorithm in use before the
Quadratic Sieve Factorization Method was developed.
See also Prime Factorization Algorithms, Smooth Number
References
Lehmer, D. H. and Powers, R. E. ``On Factoring Large Numbers.'' Bull. Amer. Math. Soc. 37, 770-776, 1931.
Morrison, M. A. and Brillhart, J. ``A Method of Factoring and the Factorization of 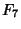 .'' Math. Comput. 29, 183-205, 1975.
.'' Math. Comput. 29, 183-205, 1975.
Pomerance, C. ``A Tale of Two Sieves.'' Not. Amer. Math. Soc. 43, 1473-1485, 1996.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , look for Integers
, look for Integers ![]() and
and ![]() such that
such that ![]() . Then
. Then
![]() and
and ![]() satisfying
satisfying
![]() .'' Math. Comput. 29, 183-205, 1975.
.'' Math. Comput. 29, 183-205, 1975.