Given a sequence of independent random variates 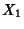 ,
, 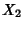 , ..., if
, ..., if
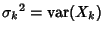 and
and
then
This means that if the Lindeberg Condition holds for the sequence of variates 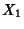 , ..., then the
Variance of an individual term in the sum
, ..., then the
Variance of an individual term in the sum 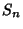 of
of 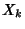 is asymptotically negligible. For such sequences, the
Lindeberg Condition is Necessary as well as Sufficient for the
Lindeberg-Feller Central Limit Theorem to hold.
is asymptotically negligible. For such sequences, the
Lindeberg Condition is Necessary as well as Sufficient for the
Lindeberg-Feller Central Limit Theorem to hold.
References
Zabell, S. L. ``Alan Turing and the Central Limit Theorem.'' Amer. Math. Monthly 102, 483-494, 1995.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() ,
, ![]() , ..., if
, ..., if
![]() and
and