If 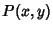 and
and 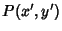 are two points on an Ellipse
are two points on an Ellipse
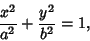 |
(1) |
with Eccentric Angles 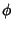 and
and 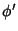 such that
such that
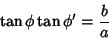 |
(2) |
and 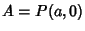 and
and 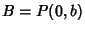 . Then
. Then
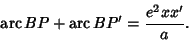 |
(3) |
This follows from the identity
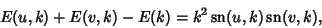 |
(4) |
where 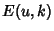 is an incomplete Elliptic Integral of the Second Kind,
is an incomplete Elliptic Integral of the Second Kind, 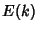 is a complete Elliptic Integral
of the Second Kind, and
is a complete Elliptic Integral
of the Second Kind, and
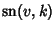 is a Jacobi Elliptic Function. If
is a Jacobi Elliptic Function. If 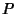 and
and 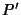 coincide, the point where they coincide is called Fagnano's Point.
coincide, the point where they coincide is called Fagnano's Point.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and
and ![]() are two points on an Ellipse
are two points on an Ellipse