|
|
|
A two-coloring of a Complete Graph ![]() of
of ![]() nodes which contains exactly the number
nodes which contains exactly the number
![]() of
Monochromatic Forced Triangles and no more (i.e., a minimum of
of
Monochromatic Forced Triangles and no more (i.e., a minimum of ![]() where
where ![]() and
and
![]() are the numbers of red and blue Triangles). Goodman (1959) showed that for an extremal graph,
are the numbers of red and blue Triangles). Goodman (1959) showed that for an extremal graph,
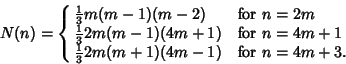
See also Bichromatic Graph, Blue-Empty Graph, Goodman's Formula, Monochromatic Forced Triangle, Schwenk's Formula
References
Goodman, A. W. ``On Sets of Acquaintances and Strangers at Any Party.'' Amer. Math. Monthly 66, 778-783, 1959.
Schwenk, A. J. ``Acquaintance Party Problem.'' Amer. Math. Monthly 79, 1113-1117, 1972.
Sloane, N. J. A. Sequence
A014557
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.