|
|
|
Given a Formula ![]() with an Absolute Error in
with an Absolute Error in ![]() of
of ![]() , the Absolute Error is
, the Absolute Error is ![]() . The
Relative Error is
. The
Relative Error is ![]() . If
. If ![]() , then
, then
| (1) |
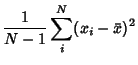 |
|||
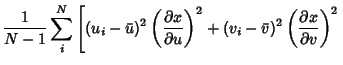 |
|||
![$\displaystyle \left.{\mathop{+}2(u_i-\bar u)(v_i-\bar v)\left({\partial x\over \partial u}\right)\left({\partial x\over \partial v}\right)+ \ldots}\right].$](e_1763.gif) |
(2) |
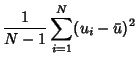 |
(3) | ||
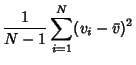 |
(4) | ||
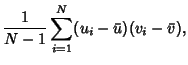 |
(5) |
| (6) |
| (7) |
Now consider addition of quantities with errors.
For ![]() ,
,
![]() and
and
![]() , so
, so
| (8) |
For division of quantities with
![]() ,
,
![]() and
and
![]() , so
, so
| (9) |
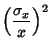 |
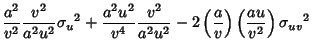 |
||
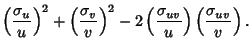 |
(10) |
For exponentiation of quantities with
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
For Logarithms of quantities with
![]() ,
,
![]() , so
, so
| (16) |
| (17) |
For multiplication with
![]() ,
,
![]() and
and
![]() , so
, so
| (18) |
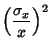 |
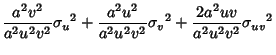 |
||
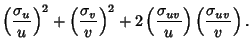 |
(19) |
For Powers,
with ![]() ,
,
![]() , so
, so
| (20) |
| (21) |
See also Absolute Error, Percentage Error, Relative Error
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 14, 1972.
Bevington, P. R. Data Reduction and Error Analysis for the Physical Sciences. New York:
McGraw-Hill, pp. 58-64, 1969.
|
|
|
© 1996-9 Eric W. Weisstein