|
|
|
The first solution to Lamé's Differential Equation, denoted ![]() for
for ![]() ,
...,
,
..., ![]() . They are also called Lamé Functions. The product of two ellipsoidal harmonics of
the first kind is a Spherical Harmonic. Whittaker and Watson (1990, pp. 536-537) write
. They are also called Lamé Functions. The product of two ellipsoidal harmonics of
the first kind is a Spherical Harmonic. Whittaker and Watson (1990, pp. 536-537) write
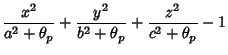 |
(1) | ||
| (2) |
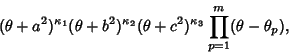 |
(3) |
| (4) |
Byerly (1959) uses the Recurrence Relations to explicitly
compute some ellipsoidal harmonics, which he denotes by ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ,
,
![\begin{eqnarray*}
K_0(x)&=&1\\
L_0(x)&=&0\\
M_0(x)&=&0\\
N_0(x)&=&0\\
K...
...^2)^2-5b^2c^2}\,)]\\
M_3^{q_3}(x)&=&x\sqrt{(x^2-b^2)(x^2-c^2)}
\end{eqnarray*}](e_708.gif)
See also Ellipsoidal Harmonic of the Second Kind, Stieltjes' Theorem
References
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics,
with Applications to Problems in Mathematical Physics. New York: Dover, pp. 254-258, 1959.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, 1990.