|
|
|
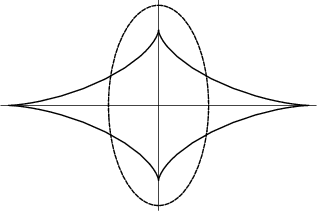
The Evolute of an Ellipse is given by the parametric equations
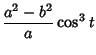 |
(1) | ||
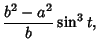 |
(2) |
|
|
|
|
|
(3) |
See also Astroid, Ellipse, Evolute, Lamé Curve
References
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, p. 77, 1993.