|
|
|
A linear Polynomial of Dyads
![]() consisting of nine components
consisting of nine components ![]() which
transform as
which
transform as
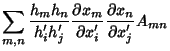 |
(1) | ||
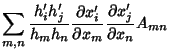 |
(2) | ||
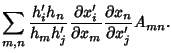 |
(3) |
A unit dyadic is also called the Idemfactor and is defined such that
| (4) |
| (5) |
| (6) |
See also Dyad, Tetradic
References
Arfken, G. ``Dyadics.'' §3.5 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 137-140, 1985.
Morse, P. M. and Feshbach, H. ``Dyadics and Other Vector Operators.'' §1.6 in
Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 54-92, 1953.