The divergence of a Vector Field 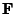 is given by
is given by
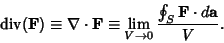 |
(1) |
Define
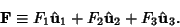 |
(2) |
Then in arbitrary orthogonal Curvilinear Coordinates,
![\begin{displaymath}
{\rm div}(F) \equiv \nabla \cdot {\bf F} \equiv {1\over h_1h...
...h_3h_1F_2) + {\partial \over \partial u_3}(h_1h_2F_3)}\right].
\end{displaymath}](d2_1068.gif) |
(3) |
If
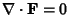 , then the field is said to be a Divergenceless Field. For divergence in individual
coordinate systems, see Curvilinear Coordinates.
, then the field is said to be a Divergenceless Field. For divergence in individual
coordinate systems, see Curvilinear Coordinates.
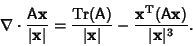 |
(4) |
The divergence of a Tensor 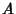 is
is
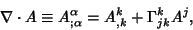 |
(5) |
where
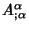 is the Covariant Derivative and
is the Covariant Derivative and 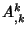 is the Comma Derivative. Expanding the terms gives
is the Comma Derivative. Expanding the terms gives
See also Curl, Curl Theorem, Gradient, Green's Theorem, Divergence Theorem,
Vector Derivative
References
Arfken, G. ``Divergence, 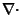 .'' §1.7 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 37-42, 1985.
.'' §1.7 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 37-42, 1985.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() is given by
is given by
![]() .'' §1.7 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 37-42, 1985.
.'' §1.7 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 37-42, 1985.