An array 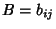 ,
, 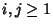 of Positive Integers is called a dispersion if
of Positive Integers is called a dispersion if
- 1. The first column of
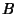 is a strictly increasing sequence, and there exists a strictly increasing sequence
is a strictly increasing sequence, and there exists a strictly increasing sequence
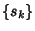 such that
such that
- 2.
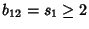 ,
,
- 3. The complement of the Set
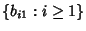 is the Set
is the Set 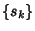 ,
,
- 4.
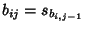 for all
for all 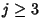 for
for 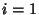 and for all
and for all 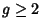 for all
for all 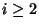 .
.
If an array 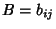 is a dispersion, then it is an Interspersion.
is a dispersion, then it is an Interspersion.
See also Interspersion
References
Kimberling, C. ``Interspersions and Dispersions.'' Proc. Amer. Math. Soc. 117, 313-321, 1993.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() ,
, ![]() of Positive Integers is called a dispersion if
of Positive Integers is called a dispersion if