Also known as Thomson's Principle. There exists a function 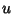 that minimizes the functional
that minimizes the functional
(called the Dirichlet Integral) for
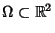 or
or 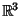 among all the
functions
among all the
functions
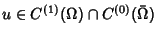 which take on given values
which take on given values 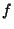 on the boundary
on the boundary
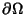 of
of
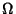 , and that function
, and that function 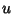 satisfies
satisfies 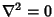 in
in 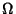 ,
,
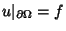 ,
,
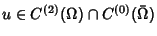 . Weierstraß
. Weierstraß  showed that Dirichlet's argument contained a subtle fallacy.
As a result, it can be claimed only that there exists a lower bound to which
showed that Dirichlet's argument contained a subtle fallacy.
As a result, it can be claimed only that there exists a lower bound to which ![$D[u]$](d2_361.gif) comes arbitrarily close without being
forced to actually reach it. Kneser, however, obtained a valid proof of Dirichlet's principle.
comes arbitrarily close without being
forced to actually reach it. Kneser, however, obtained a valid proof of Dirichlet's principle.
See also Dirichlet's Box Principle, Dirichlet Integrals
© 1996-9 Eric W. Weisstein
1999-05-24
![]() that minimizes the functional
that minimizes the functional