Darboux Integral

A variant of the Riemann Integral defined when the Upper and Lower Integrals, taken as limits of the Lower Sum

$$L(f;\phi;N)=\sum_{r=1}^n m(f;\delta_r)-\phi(x_{r-1})$$

and Upper Sum

$$U(f;\phi;N)=\sum_{r=1}^n M(f;\delta_r)-\phi(x_{r-1}),$$

are equal. Here, $f(x)$ is a Real Function, $\phi(x)$ is a monotonic increasing function with respect to which the sum is taken, $m(f;S)$ denotes the lower bound of $f(x)$ over the interval $S$, and $M(f;S)$ denotes the upper bound.

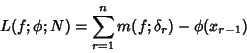
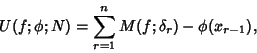
See also Lower Integral, Lower Sum, Riemann Integral, Upper Integral, Upper Sum

References

Kestelman, H. Modern Theories of Integration, 2nd rev. ed. New York: Dover, p. 250, 1960.