An 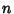 -cycle is a finite sequence of points
-cycle is a finite sequence of points 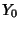 , ...,
, ..., 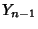 such that, under a Map
such that, under a Map 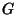 ,
,
In other words, it is a periodic trajectory which comes back to the same point after 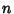 iterations of the cycle. Every
point
iterations of the cycle. Every
point 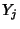 of the cycle satisfies
of the cycle satisfies
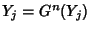 and is therefore a Fixed Point of the mapping
and is therefore a Fixed Point of the mapping 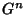 . A fixed
point of
. A fixed
point of 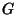 is simply a Cycle of period 1.
is simply a Cycle of period 1.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() -cycle is a finite sequence of points
-cycle is a finite sequence of points ![]() , ...,
, ..., ![]() such that, under a Map
such that, under a Map ![]() ,
,