|
|
|
A cusp form is a Modular Form for which the coefficient ![]() in the Fourier Series
in the Fourier Series
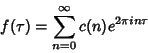
See also Modular Form
References
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag,
pp. 114 and 116, 1997.