A group generated by the elements 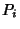 for
for 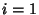 , ...,
, ..., 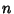 subject to
subject to
where 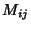 are the elements of a Coxeter Matrix. Coxeter used the Notation
are the elements of a Coxeter Matrix. Coxeter used the Notation ![$[3^{p,q,r}]$](c3_724.gif) for the
Coxeter group generated by the nodes of a Y-shaped Coxeter-Dynkin Diagram whose three arms have
for the
Coxeter group generated by the nodes of a Y-shaped Coxeter-Dynkin Diagram whose three arms have 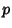 ,
, 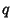 , and
, and
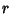 Edges. A Coxeter group of this form is finite Iff
Edges. A Coxeter group of this form is finite Iff
See also Bimonster
References
Arnold, V. I. ``Snake Calculus and Combinatorics of Bernoulli, Euler, and Springer Numbers for Coxeter Groups.''
Russian Math. Surveys 47, 3-45, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() for
for ![]() , ...,
, ..., ![]() subject to
subject to