Cornu Spiral

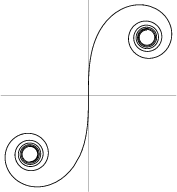
$\begin{figure}\begin{center}\BoxedEPSF{cornu_spiral.epsf scaled 600}\end{center}\end{figure}$

A plot in the Complex Plane of the points

$\begin{displaymath} B(z) = C(t)+iS(t)=\int_0^t e^{i\pi x^2/2}\,dx, \end{displaymath}$

(1)

where

and

are the Fresnel Integrals. The Cornu spiral is also known as the Clothoid or Euler's Spiral. A Cornu spiral describes diffraction from the edge of a half-plane.

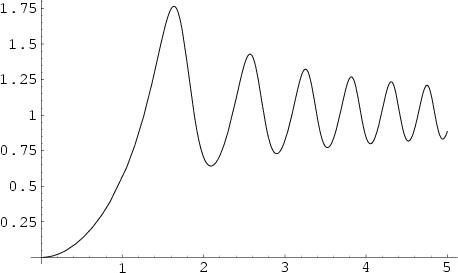
$\begin{figure}\begin{center}\BoxedEPSF{CornuSlope.epsf}\end{center}\end{figure}$

The Slope of the Cornu spiral

$\begin{displaymath} m(t)={S(t)\over C(t)} \end{displaymath}$

(2)

is plotted above.

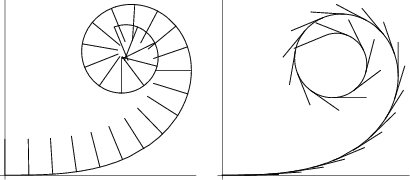
$\begin{figure}\begin{center}\BoxedEPSF{CornuNormalTangent.epsf}\end{center}\end{figure}$

The Slope of the curve's Tangent Vector (above right figure) is

$\begin{displaymath} m_T(t)={S'(t)\over C'(t)}=\tan({\textstyle{1\over 2}}\pi t^2), \end{displaymath}$

(3)

plotted below.

$\begin{figure}\begin{center}\BoxedEPSF{CornuTangentSlope.epsf}\end{center}\end{figure}$

The Cesàro Equation for a Cornu spiral is $\rho=c^2/s$ , where $\rho$ is the Radius of Curvature and the Arc Length. The Torsion is $\tau=0$ .

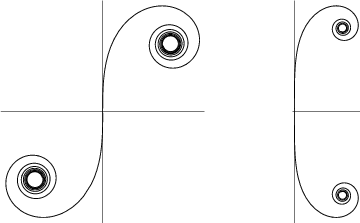
$\begin{figure}\begin{center}\BoxedEPSF{CornuSpirals.epsf}\end{center}\end{figure}$

Gray (1993) defines a generalization of the Cornu spiral given by parametric equations

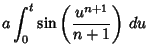$\displaystyle x(t)$	$\textstyle =$	$\displaystyle a\int_0^t \sin\left({u^{n+1}\over n+1}\right)\,du$	(4)
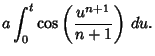$\displaystyle y(t)$	$\textstyle =$	$\displaystyle a\int_0^t \cos\left({u^{n+1}\over n+1}\right)\,du.$	(5)

$\begin{figure}\begin{center}\BoxedEPSF{CornuSpiralInfo.epsf scaled 700}\end{center}\end{figure}$

The Arc Length, Curvature, and Tangential Angle of this curve are

$\displaystyle s(t)$	$\textstyle =$	$\displaystyle at$	(6)
$\displaystyle \kappa(t)$	$\textstyle =$	$\displaystyle -{t^n\over a}$	(7)
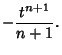$\displaystyle \phi(t)$	$\textstyle =$	$\displaystyle -{t^{n+1}\over n+1}.$	(8)

The Cesàro Equation is

$\begin{displaymath} \kappa=-{a\over s^n}. \end{displaymath}$

(9)

Dillen (1990) describes a class of ``polynomial spirals'' for which the Curvature is a polynomial function of the Arc Length. These spirals are a further generalization of the Cornu spiral.

See also Fresnel Integrals, Nielsen's Spiral

References

Dillen, F. ``The Classification of Hypersurfaces of a Euclidean Space with Parallel Higher Fundamental Form.'' Math. Z. 203, 635-643, 1990.

Gray, A. ``Clothoids.'' §3.6 in Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 50-52, 1993.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 190-191, 1972.