A quantity also known as a Christoffel Symbol of the Second Kind.
Connection Coefficients are defined by
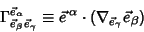 |
(1) |
(long form) or
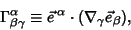 |
(2) |
(abbreviated form), and satisfy
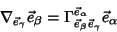 |
(3) |
(long form) and
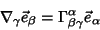 |
(4) |
(abbreviated form).
Connection Coefficients are not Tensors, but have Tensor-like Contravariant and Covariant indices. A fully Covariant
connection Coefficient is given by
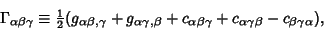 |
(5) |
where the 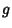 s are the Metric Tensors, the
s are the Metric Tensors, the 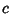 s are Commutation Coefficients, and the commas indicate the Comma Derivative. In an Orthonormal Basis,
s are Commutation Coefficients, and the commas indicate the Comma Derivative. In an Orthonormal Basis,
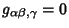 and
and
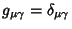 , so
, so
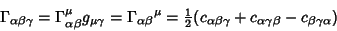 |
(6) |
and
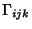 |
 |
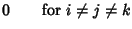 |
(7) |
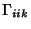 |
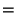 |
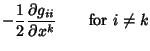 |
(8) |
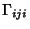 |
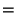 |
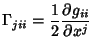 |
(9) |
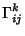 |
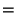 |
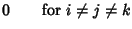 |
(10) |
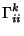 |
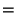 |
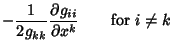 |
(11) |
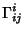 |
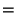 |
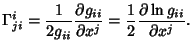 |
(12) |
For Tensors of Rank 3, the connection Coefficients may be
concisely summarized in Matrix form:
![\begin{displaymath}
\Gamma^\theta \equiv \left[{\matrix{ \Gamma^\theta_{rr} & \G...
...^\theta_{\phi \phi}\cr}}\right].
\hrule width 0pt height 5.9pt
\end{displaymath}](c2_1391.gif) |
(13) |
Connection Coefficients arise in the computation of Geodesics. The Geodesic
Equation of free motion is
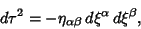 |
(14) |
or
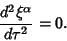 |
(15) |
Expanding,
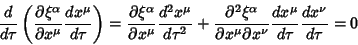 |
(16) |
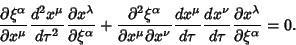 |
(17) |
But
 |
(18) |
so
 |
(19) |
where
 |
(20) |
See also Cartan Torsion Coefficient, Christoffel Symbol of the First Kind, Christoffel Symbol of the
Second Kind, Comma Derivative, Commutation Coefficient, Curvilinear Coordinates, Semicolon
Derivative, Tensor
© 1996-9 Eric W. Weisstein
1999-05-26
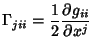
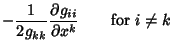
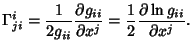
![\begin{displaymath}
\Gamma^\theta \equiv \left[{\matrix{ \Gamma^\theta_{rr} & \G...
...^\theta_{\phi \phi}\cr}}\right].
\hrule width 0pt height 5.9pt
\end{displaymath}](c2_1391.gif)