|
|
|
Variously denoted
![]() or
or ![]() .
.
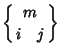 |
![$\displaystyle \Gamma^m_{ij} = \vec e\,^m \cdot {\partial \vec e_i\over \partial q^j} = g^{km}[ij,k]$](c1_1664.gif) |
||
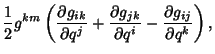 |
(1) |
| (2) |
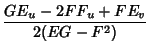 |
(3) | ||
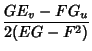 |
(4) | ||
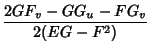 |
(5) | ||
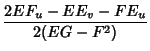 |
(6) | ||
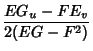 |
(7) | ||
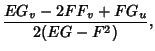 |
(8) |
| (9) | |||
| (10) | |||
| (11) | |||
| (12) | |||
| (13) | |||
| (14) |
The following relationships hold between the Christoffel symbols of the second kind and coefficients of the first
Fundamental Form,
| (15) | |||
| (16) | |||
| (17) | |||
| (18) | |||
| (19) | |||
| (20) | |||
| (21) | |||
| (22) |
For a surface given in Monge's Form ![]() ,
,
| (23) |
See also Christoffel Symbol of the First Kind, Connection Coefficient, Gauss Equations
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press,
pp. 160-167, 1985.
Gray, A. ``Christoffel Symbols.'' §20.3 in
Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press,
pp. 397-400, 1993.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I.
New York: McGraw-Hill, pp. 47-48, 1953.
|
|
|
© 1996-9 Eric W. Weisstein