Congruent Isoscelizers Point

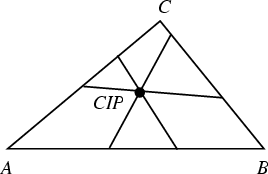
$\begin{figure}\begin{center}\BoxedEPSF{CongruentIsoscelizers.epsf}\end{center}\end{figure}$

In 1989, P. Yff proved there is a unique configuration of Isoscelizers for a given Triangle such that all three have the same length. Furthermore, these Isoscelizers meet in a point called the congruent isoscelizers point, which has Triangle Center Function

$\begin{displaymath} \alpha=\cos({\textstyle{1\over 2}}B)+\cos({\textstyle{1\over 2}}C)-\cos({\textstyle{1\over 2}}A). \end{displaymath}$

See also Isoscelizer

References

Kimberling, C. ``Congruent Isoscelizers Point.'' http://cedar.evansville.edu/~ck6/tcenters/recent/conisos.html.