|
|
|
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
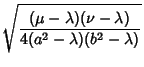 |
(7) | ||
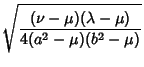 |
(8) | ||
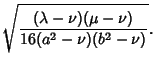 |
(9) |
|
|
|
|
|
|
|
|
|
|
|
(10) |
See also Helmholtz Differential Equation--Confocal Paraboloidal Coordinates
References
Arfken, G. ``Confocal Parabolic Coordinates (
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 664, 1953.
![]() ,
, ![]() ,
, ![]() ).'' §2.17 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 119-120, 1970.
).'' §2.17 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 119-120, 1970.