|
|
|
Let ![]() be the Principal (initial investment),
be the Principal (initial investment), ![]() be the annual compounded rate,
be the annual compounded rate, ![]() the ``nominal rate,''
the ``nominal rate,''
![]() be the number of times Interest is compounded per year (i.e., the year is divided into
be the number of times Interest is compounded per year (i.e., the year is divided into ![]() Conversion
Periods), and
Conversion
Periods), and ![]() be the number of years (the ``term''). The Interest rate per Conversion
Period is then
be the number of years (the ``term''). The Interest rate per Conversion
Period is then
| (1) |
| (2) |
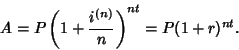 |
(3) |
| (4) |
The time required for a given Principal to double (assuming ![]() Conversion Period) is given by solving
Conversion Period) is given by solving
| (5) |
| (6) |
| (7) |
See also e, Interest, Ln, Natural Logarithm, Principal, Rule of 72, Simple Interest
References
Kellison, S. G. The Theory of Interest, 2nd ed. Burr Ridge, IL: Richard D. Irwin, pp. 14-16, 1991.
Milanfar, P. ``A Persian Folk Method of Figuring Interest.'' Math. Mag. 69, 376, 1996.
|
|
|
© 1996-9 Eric W. Weisstein