A Set 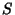 and a Binary Operator
and a Binary Operator 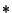 are said to exhibit closure if applying
the Binary Operator to two elements
are said to exhibit closure if applying
the Binary Operator to two elements 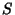 returns a value which is itself a member of
returns a value which is itself a member of 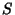 .
.
The term ``closure'' is also used to refer to a ``closed'' version of a given set. The closure of a Set can be defined
in several equivalent ways, including
- 1. The Set plus its Limit Points, also called ``boundary'' points, the union of
which is also called the ``frontier,''
- 2. The unique smallest Closed Set containing the given Set,
- 3. The Complement of the interior of the Complement of the set,
- 4. The collection of all points such that every Neighborhood of them intersects the original Set in a
nonempty Set.
In topologies where the T2-Separation Axiom is assumed, the closure of a finite Set 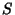 is
is 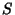 itself.
itself.
See also Binary Operator, Existential Closure, Reflexive Closure, Tight Closure, Transitive Closure
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and a Binary Operator
and a Binary Operator ![]() are said to exhibit closure if applying
the Binary Operator to two elements
are said to exhibit closure if applying
the Binary Operator to two elements ![]() returns a value which is itself a member of
returns a value which is itself a member of ![]() .
.