A 1-D Map which maps a Circle onto itself
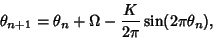 |
(1) |
where 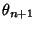 is computed mod 1. Note that the circle map has two parameters:
is computed mod 1. Note that the circle map has two parameters: 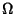 and
and 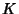 .
. 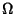 can be
interpreted as an externally applied frequency, and
can be
interpreted as an externally applied frequency, and 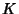 as a strength of nonlinearity. The 1-D Jacobian is
as a strength of nonlinearity. The 1-D Jacobian is
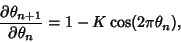 |
(2) |
so the circle map is not Area-Preserving. It is related to the Standard Map
for 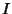 and
and 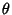 computed mod 1. Writing
computed mod 1. Writing 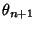 as
as
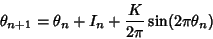 |
(5) |
gives the circle map with 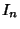 =
= 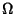 and
and 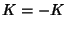 . The unperturbed circle map has the form
. The unperturbed circle map has the form
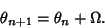 |
(6) |
If 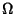 is Rational, then it is known as the map Winding Number, defined by
is Rational, then it is known as the map Winding Number, defined by
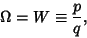 |
(7) |
and implies a periodic trajectory, since 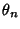 will return to the same point (at most) every
will return to the same point (at most) every 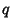 Orbits. If
Orbits. If 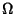 is Irrational, then the motion is quasiperiodic. If
is Irrational, then the motion is quasiperiodic. If 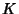 is Nonzero,
then the motion may be periodic in some finite region surrounding each Rational
is Nonzero,
then the motion may be periodic in some finite region surrounding each Rational 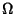 . This
execution of periodic motion in response to an Irrational forcing is known as Mode
Locking.
. This
execution of periodic motion in response to an Irrational forcing is known as Mode
Locking.
If a plot is made of 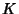 vs.
vs. 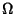 with the regions of periodic Mode-Locked parameter space
plotted around Rational
with the regions of periodic Mode-Locked parameter space
plotted around Rational 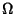 values (Winding Numbers), then the regions are seen to widen upward from 0 at
values (Winding Numbers), then the regions are seen to widen upward from 0 at 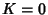 to
some finite width at
to
some finite width at 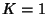 . The region surrounding each Rational Number is known as an Arnold Tongue. At
. The region surrounding each Rational Number is known as an Arnold Tongue. At 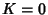 , the Arnold Tongues are an isolated set of Measure zero. At
, the Arnold Tongues are an isolated set of Measure zero. At 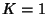 , they form a
Cantor Set of Dimension
, they form a
Cantor Set of Dimension
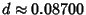 . For
. For 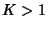 , the tongues overlap, and the circle map becomes
noninvertible. The circle map has a Feigenbaum Constant
, the tongues overlap, and the circle map becomes
noninvertible. The circle map has a Feigenbaum Constant
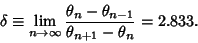 |
(8) |
See also Arnold Tongue, Devil's Staircase, Mode Locking, Winding Number (Map)
© 1996-9 Eric W. Weisstein
1999-05-26
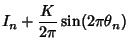
![]() vs.
vs. ![]() with the regions of periodic Mode-Locked parameter space
plotted around Rational
with the regions of periodic Mode-Locked parameter space
plotted around Rational ![]() values (Winding Numbers), then the regions are seen to widen upward from 0 at
values (Winding Numbers), then the regions are seen to widen upward from 0 at ![]() to
some finite width at
to
some finite width at ![]() . The region surrounding each Rational Number is known as an Arnold Tongue. At
. The region surrounding each Rational Number is known as an Arnold Tongue. At ![]() , the Arnold Tongues are an isolated set of Measure zero. At
, the Arnold Tongues are an isolated set of Measure zero. At ![]() , they form a
Cantor Set of Dimension
, they form a
Cantor Set of Dimension
![]() . For
. For ![]() , the tongues overlap, and the circle map becomes
noninvertible. The circle map has a Feigenbaum Constant
, the tongues overlap, and the circle map becomes
noninvertible. The circle map has a Feigenbaum Constant