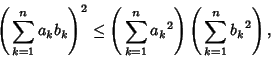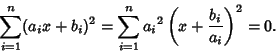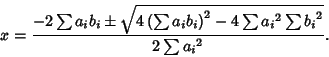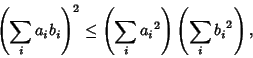A special case of the Hölder Sum Inequality with 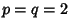 ,
,
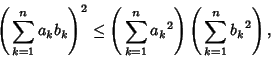 |
(1) |
where equality holds for 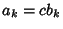 . In 2-D, it becomes
. In 2-D, it becomes
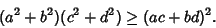 |
(2) |
It can be proven by writing
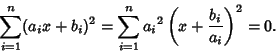 |
(3) |
If 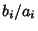 is a constant
is a constant 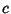 , then
, then 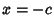 . If it is not a constant, then all terms cannot simultaneously vanish for
Real
. If it is not a constant, then all terms cannot simultaneously vanish for
Real 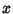 , so the solution is Complex and can be found using the
Quadratic Equation
, so the solution is Complex and can be found using the
Quadratic Equation
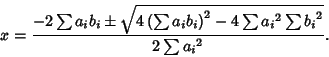 |
(4) |
In order for this to be Complex, it must be true that
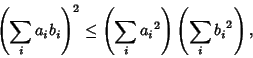 |
(5) |
with equality when 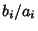 is a constant. The Vector derivation is much simpler,
is a constant. The Vector derivation is much simpler,
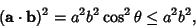 |
(6) |
where
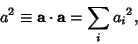 |
(7) |
and similarly for 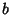 .
.
See also Chebyshev Inequality, Hölder Sum Inequality
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 11, 1972.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() ,
,