|
|
|

A Fractal which can be constructed using String Rewriting by creating a matrix three times the size of the current matrix using the rules
The first three steps are illustrated above.
The size of the unit element after the ![]() th iteration is
th iteration is
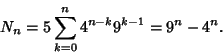
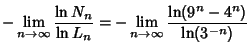 |
|||
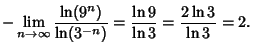 |
See also Box Fractal, Cantor Dust
References
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press,
pp. 82-83, 1991.
![]() Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.
Weisstein, E. W. ``Fractals.'' Mathematica notebook Fractal.m.