|
|
|
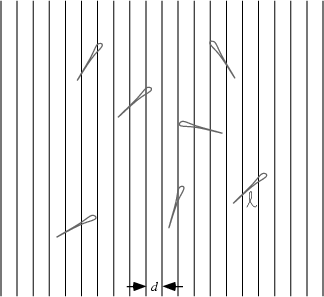
Find the probability ![]() that a needle of length
that a needle of length ![]() will land on a line, given a floor with equally spaced Parallel
Lines a distance
will land on a line, given a floor with equally spaced Parallel
Lines a distance ![]() apart.
apart.
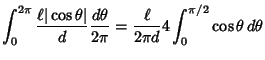 |
|||
![$\displaystyle {2\ell\over \pi d} [\sin\theta]^{\pi/2}_0 = {2\ell\over \pi d}.$](b_2414.gif) |
See also Buffon-Laplace Needle Problem
References
Badger, L. ``Lazzarini's Lucky Approximation of
Dörrie, H. ``Buffon's Needle Problem.'' §18 in
100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 73-77, 1965.
Kraitchik, M. ``The Needle Problem.'' §6.14 in Mathematical Recreations. New York: W. W. Norton,
p. 132, 1942.
Wegert, E. and Trefethen, L. N. ``From the Buffon Needle Problem to the Kreiss Matrix Theorem.''
Amer. Math. Monthly 101, 132-139, 1994.
![]() .'' Math. Mag. 67, 83-91, 1994.
.'' Math. Mag. 67, 83-91, 1994.