A Tschirnhausen Transformation can be used to algebraically transform a general Quintic Equation to the form
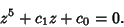 |
(1) |
In practice, the general quintic is first reduced to the Principal Quintic Form
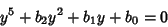 |
(2) |
before the transformation is done. Then, we require that the sum of the third Powers of the
Roots vanishes, so 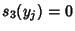 . We assume that the Roots
. We assume that the Roots 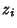 of the Bring-Jerrard
quintic are related to the Roots
of the Bring-Jerrard
quintic are related to the Roots 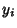 of the Principal Quintic Form by
of the Principal Quintic Form by
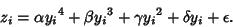 |
(3) |
In a similar manner to the Principal Quintic Form transformation, we can express the
Coefficients 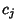 in terms of the
in terms of the 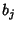 .
.
See also Bring Quintic Form, Principal Quintic Form, Quintic Equation
© 1996-9 Eric W. Weisstein
1999-05-26