Use the definition of the q-Series
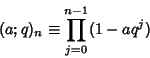 |
(1) |
and define
![\begin{displaymath}
\left[{\matrix{N\cr M\cr}}\right] \equiv {(q^{N-M+1}; q)_M\over (q; q)_m}.
\end{displaymath}](b_1859.gif) |
(2) |
Then P. Borwein has conjectured that (1) the Polynomials 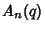 ,
, 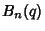 , and
, and 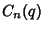 defined by
defined by
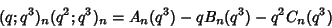 |
(3) |
have Nonnegative Coefficients, (2) the Polynomials 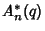 ,
,
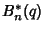 , and
, and 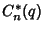 defined by
defined by
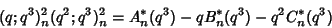 |
(4) |
have Nonnegative Coefficients, (3) the Polynomials 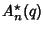 ,
,
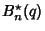 ,
, 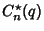 ,
, 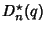 , and
, and 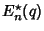 defined by
defined by
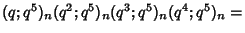
|
|
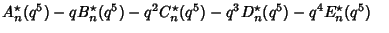
|
(5) |
have Nonnegative Coefficients, (4) the Polynomials
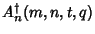 ,
,
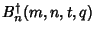 , and
, and
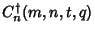 defined by
defined by
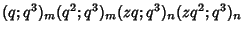
|
|
![$ =\sum_{t=0}^{2m} z^t[A^\dagger(m,n,t,q^3)-qB^\dagger(m,n,t,q^3)-q^2C^\dagger(m,n,t,q^3)]\quad$](b_1879.gif)
|
(6) |
have Nonnegative Coefficients, (5) for 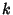 Odd and
Odd and
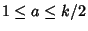 ,
consider the expansion
,
consider the expansion
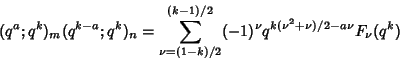 |
(7) |
with
![\begin{displaymath}
F_\nu(q)=\sum_{j=-\infty}^\infty (-1)^j q^{j(k^2j+2k\nu+k-2a)/2}\left[{\matrix{m+n\cr m+\nu+kj\cr}}\right],
\end{displaymath}](b_1882.gif) |
(8) |
then if 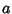 is Relatively Prime to
is Relatively Prime to 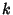 and
and 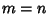 , the Coefficients of
, the Coefficients of 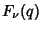 are Nonnegative, and (6) given
are Nonnegative, and (6) given
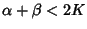 and
and
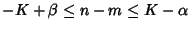 , consider
, consider
![\begin{displaymath}
G(\alpha,\beta,K;q)=\sum_q(-1)^j q^{j[K(\alpha+\beta)j+K(\alpha+\beta)]/2}\left[{\matrix{m+n\cr m+Kj\cr}}\right],
\end{displaymath}](b_1886.gif) |
(9) |
the Generating Function for partitions inside an 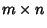 rectangle with hook difference conditions specified by
rectangle with hook difference conditions specified by
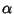 ,
, 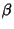 , and
, and 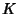 . Let
. Let 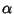 and
and 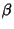 be Positive Rational Numbers and
be Positive Rational Numbers and 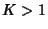 an
Integer such that
an
Integer such that 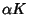 and
and 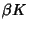 are integers. Then if
are integers. Then if
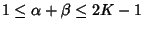 (with strict
inequalities for
(with strict
inequalities for 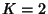 ) and
) and
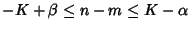 , then
, then
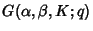 has Nonnegative
Coefficients.
has Nonnegative
Coefficients.
See also q-Series
References
Andrews, G. E. et al. ``Partitions with Prescribed Hook Differences.'' Europ. J. Combin. 8, 341-350, 1987.
Bressoud, D. M. ``The Borwein Conjecture and Partitions with Prescribed Hook Differences.'' Electronic J. Combinatorics 3, No. 2, R4, 1-14, 1996.
http://www.combinatorics.org/Volume_3/volume3_2.html#R4.
© 1996-9 Eric W. Weisstein
1999-05-26
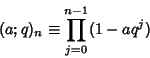
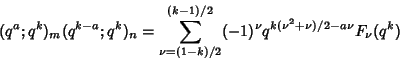
![\begin{displaymath}
F_\nu(q)=\sum_{j=-\infty}^\infty (-1)^j q^{j(k^2j+2k\nu+k-2a)/2}\left[{\matrix{m+n\cr m+\nu+kj\cr}}\right],
\end{displaymath}](b_1882.gif)
![\begin{displaymath}
G(\alpha,\beta,K;q)=\sum_q(-1)^j q^{j[K(\alpha+\beta)j+K(\alpha+\beta)]/2}\left[{\matrix{m+n\cr m+Kj\cr}}\right],
\end{displaymath}](b_1886.gif)