Bohr-Favard Inequalities

If $f$ has no spectrum in $[-\lambda, \lambda]$, then

$$\vert\vert f\vert\vert _\infty \leq {\pi\over 2\lambda} \vert\vert f'\vert\vert _\infty$$

(Bohr 1935). A related inequality states that if $A_k$ is the class of functions such that

$$f(x)=f(x+2\pi), f(x), f'(x), \ldots, f^{(k-1)}(x)$$

are absolutely continuous and $\int_0^{2\pi} f(x)\,dx=0$, then

$$\vert\vert f\vert\vert _\infty \leq{4\over\pi}\sum_{\nu=0}^\... ...}\over (2\nu+1)^{k+1}} \vert\vert f^{(k)}(x)\vert\vert _\infty$$

(Northcott 1939). Further, for each value of $k$, there is always a function $f(x)$ belonging to $A_k$ and not identically zero, for which the above inequality becomes an equality (Favard 1936). These inequalities are discussed in Mitrinovic et al. (1991).

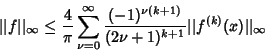
References

Bohr, H. ``Ein allgemeiner Satz über die Integration eines trigonometrischen Polynoms.'' Prace Matem.-Fiz. 43, 1935.

Favard, J. ``Application de la formule sommatoire d'Euler à la démonstration de quelques propriétés extrémales des intégrale des fonctions périodiques ou presquepériodiques.'' Mat. Tidsskr. B, 81-94, 1936. [Reviewed in Zentralblatt f. Math. 16, 58-59, 1939.]

Mitrinovic, D. S.; Pecaric, J. E.; and Fink, A. M. Inequalities Involving Functions and Their Integrals and Derivatives. Dordrecht, Netherlands: Kluwer, pp. 71-72, 1991.

Northcott, D. G. ``Some Inequalities Between Periodic Functions and Their Derivatives.'' J. London Math. Soc. 14, 198-202, 1939.

Tikhomirov, V. M. ``Approximation Theory.'' In Analysis II. Convex Analysis and Approximation Theory (Ed. R. V. Gamkrelidze). New York: Springer-Verlag, pp. 93-255, 1990.