|
|
|
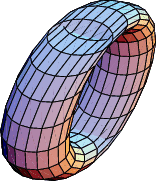
A Quartic Surface which can be constructed as follows. Given a Circle ![]() and Plane
and Plane ![]() Perpendicular to the Plane of
Perpendicular to the Plane of ![]() , move a second Circle
, move a second Circle ![]() of the same Radius as
of the same Radius as
![]() through space so that its Center always lies on
through space so that its Center always lies on ![]() and it remains Parallel to
and it remains Parallel to ![]() . Then
. Then ![]() sweeps out the Bohemian dome. It can be given by the parametric equations
sweeps out the Bohemian dome. It can be given by the parametric equations
See also Quartic Surface
References
Fischer, G. (Ed.). Mathematical Models from the Collections of Universities and Museums.
Braunschweig, Germany: Vieweg, pp. 19-20, 1986.
Fischer, G. (Ed.). Plate 50 in
Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume. Braunschweig, Germany: Vieweg, p. 50, 1986.
Nordstrand, T. ``Bohemian Dome.''
http://www.uib.no/people/nfytn/bodtxt.htm.