|
|
|
A bicubic spline is a special case of bicubic interpolation which uses an interpolation function of the form
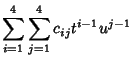 |
|||
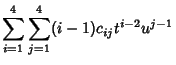 |
|||
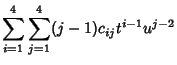 |
|||
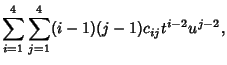 |
See also B-Spline, Spline
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 118-122, 1992.