|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
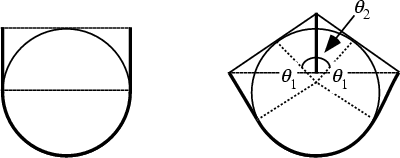
A ``beam detector'' for a given curve ![]() is defined as a curve (or set of curves) through which every Line
tangent to or intersecting
is defined as a curve (or set of curves) through which every Line
tangent to or intersecting ![]() passes. The shortest 1-arc beam detector, illustrated in the upper left figure, has length
passes. The shortest 1-arc beam detector, illustrated in the upper left figure, has length
![]() . The shortest known 2-arc beam detector, illustrated in the right figure, has angles
. The shortest known 2-arc beam detector, illustrated in the right figure, has angles
| (1) | |||
| (2) |
| (3) |
| (4) |
|
|
|
|
|
(5) |
| (6) |
References
Croft, H. T.; Falconer, K. J.; and Guy, R. K. §A30 in Unsolved Problems in Geometry. New York: Springer-Verlag, 1991.
Faber, V.; Mycielski, J.; and Pedersen, P. ``On the Shortest Curve which Meets All Lines which Meet a Circle.''
Ann. Polon. Math. 44, 249-266, 1984.
Faber, V. and Mycielski, J. ``The Shortest Curve that Meets All Lines that Meet a Convex Body.'' Amer. Math. Monthly 93,
796-801, 1986.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/beam/beam.html
Makai, E. ``On a Dual of Tarski's Plank Problem.'' In Diskrete Geometrie. 2 Kolloq., Inst. Math. Univ. Salzburg, 127-132, 1980.
Stewart, I. ``The Great Drain Robbery.'' Sci. Amer., 206-207, 106, and 125, Sept. 1995, Dec. 1995, and Feb. 1996.
|
|
|
© 1996-9 Eric W. Weisstein