|
|
|
The Map
| (1) |
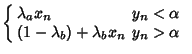 |
(2) | ||
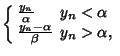 |
(3) |
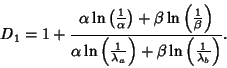 |
(4) |
| (5) |
References
Lichtenberg, A. and Lieberman, M. Regular and Stochastic Motion. New York: Springer-Verlag, p. 60, 1983.
Ott, E. Chaos in Dynamical Systems. Cambridge, England: Cambridge University Press, pp. 81-82, 1993.
Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, p. 32, 1990.