Archimedes' Spiral

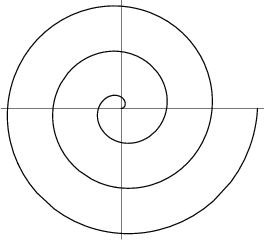
$\begin{figure}\begin{center}\BoxedEPSF{spiral_archimedes.epsf}\end{center}\end{figure}$

An Archimedean Spiral with Polar equation

$\begin{displaymath} r = a\theta. \end{displaymath}$

This spiral was studied by Conon, and later by Archimedes

in On Spirals about 225 BC.

Archimedes

was able to work out the lengths of various tangents to the spiral.

Archimedes' spiral can be used for Compass and Straightedge division of an Angle into parts (including Angle Trisection) and can also be used for Circle Squaring. In addition, the curve can be used as a cam to convert uniform circular motion into uniform linear motion. The cam consists of one arch of the spiral above the x-Axis together with its reflection in the x-Axis. Rotating this with uniform angular velocity about its center will result in uniform linear motion of the point where it crosses the y-Axis.

See also Archimedean Spiral

References

Gardner, M. The Unexpected Hanging and Other Mathematical Diversions. Chicago, IL: Chicago University Press, pp. 106-107, 1991.

Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 69-70, 1993.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 186-187, 1972.

Lockwood, E. H. A Book of Curves. Cambridge, England: Cambridge University Press, pp. 173-164, 1967.